2018半岛星空体育·(中国)官方网站数学：积分中值定理的证明

  半岛星空体育·(中国)官方网站数学有四大重要定力证明需要大家熟练掌握，它们是微分中值定理的证明、求导公式的证明、积分中值定理和微积分基本定理的证明，下文是聚英半岛星空体育·(中国)官方网站网为大家整理的积分中值定理的证明。

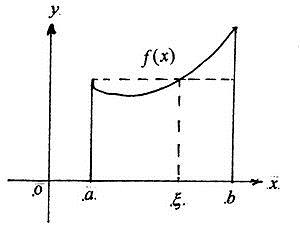
  一、积分中值定理的定义

  该定理条件是定积分的被积函数在积分区间(闭区间)上连续，结论可以形式地记成该定积分等于把被积函数拎到积分号外面，并把积分变量x换成中值。

  二、积分中值定理的证明方法

  如何证明?可能有同学想到用微分中值定理，理由是微分相关定理的结论中含有中值。可以按照此思路往下分析，不过更易理解的思路是考虑连续相关定理(介值定理和零点存在定理)，理由更充分些：上述两个连续相关定理的结论中不但含有中值而且不含导数，而待证的积分中值定理的结论也是含有中值但不含导数。

  若我们选择了用连续相关定理去证，那么到底选择哪个定理呢?这里有个小的技巧——看中值是位于闭区间还是开区间。介值定理和零点存在定理的结论中的中值分别位于闭区间和开区间，而待证的积分中值定理的结论中的中值位于闭区间。那么何去何从，已经不言自明了。

  若顺利选中了介值定理，那么往下如何推理呢?我们可以对比一下介值定理和积分中值定理的结论：介值定理的结论的等式一边为某点处的函数值，而等号另一边为常数A。我们自然想到把积分中值定理的结论朝以上的形式变形。等式两边同时除以区间长度，就能达到我们的要求。当然，变形后等号一侧含有积分的式子的长相还是挺有迷惑性的，要透过现象看本质，看清楚定积分的值是一个数，进而定积分除以区间长度后仍为一个数。这个数就相当于介值定理结论中的A。

  接下来如何推理，这就考察各位对介值定理的熟悉程度了。该定理条件有二：1.函数在闭区间连续，2.实数A位于函数在闭区间上的最大值和最小值之间，结论是该实数能被取到(即A为闭区间上某点的函数值)。再看若积分中值定理的条件成立否能推出介值定理的条件成立。函数的连续性不难判断，仅需说明定积分除以区间长度这个实数位于函数的最大值和最小值之间即可。而要考察一个定积分的值的范围，不难想到比较定理(或估值定理)。

  三、相关阅读推荐：

    2018半岛星空体育·(中国)官方网站数学：微分中值定理的证明    2018半岛星空体育·(中国)官方网站数学：求导公式的证明

  四、资讯推荐：

  2017湖南大学半岛星空体育·(中国)官方网站招生目录
  2017年华东师范大学半岛星空体育·(中国)官方网站招生目录

  更多资讯欢迎关注：

  半岛星空体育·(中国)官方网站新浪微博：聚英半岛星空体育·(中国)官方网站在线

  半岛星空体育·(中国)官方网站微信平台：聚英半岛星空体育·(中国)官方网站网（sxzykkaoyan）